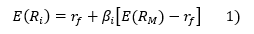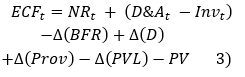Methodological note n°2 : Fairness Finance’s risk premium, the prospective approach

The formalization of the notion of market risk premium is rooted in Harry Markowitz's work (1956) on portfolio diversification and maximization of the risk/return ratio. This work completed in the 1960s by the contributions of Jack Treynor, William Sharpe, John Lintner and Jan Mossin led to the capital asset pricing model (CAPM) which establishes the link between the expected return of a risky security, its "beta" and the market risk premium according to a linear relationship, the “Security Market Line”:

 

 

where the market risk premium, [ E(R_M)  -  r_f ], is the slope of this line, with E(R_M) the mathematical expectation of the market return, and r_f the intercept of the line, equal to the risk-free rate (government bonds), and β_i is the explanatory variable, i.e. the beta specific to the security in question.

 

The product of this beta coefficient and the market risk premium constitutes the price of a security's "systematic risk" which sets its expected return in addition to the risk-free rate. This expected yield is equal to the cost of capital, as any future cash flow contributing to a security's expected return will be discounted at that rate.

 

In the CAPM, the appraisal of any risky asset thus requires knowing the value of the risk-free rate first, which is public information, as well as the market risk premium, which is not directly obvious. To estimate the market's risk premium, research has successively borrowed two complementary but opposing approaches:

• since the early days of the CAPM, the model's tests naturally led to the collection of listed stocks' past returns. Aggregating this data made it possible to establish the returns of the market as a whole. The difference between the latter and that of government bonds could thus be calculated as the average "ex-post" or "historical" or "effective" premium on the stock market.
• Since the 1980s, other approaches based on market expectations have come into use. They aim to estimate the IRR which makes the present value of corporate financial forecasts equal to their stock market price. The aggregation of these IRRs thus forms the implied cost of capital for the market as a whole. The difference between the latter and the risk-free rate is equal to the "ex-ante", "forecast" or "implied" risk premium.

• Given the variability in effective returns, ex-post risk premia may be negative, so the calculation of historical premiums must be based on long periods of observation, covering several economic cycles, or even exceptional periods such as global conflicts or the thirty-year post-war boom. Does this reflect current investor expectations? These historical premiums reflect only an average situation in relation to the business cycle. Conversely, ex-ante risk premiums are synchronized with the economic cycle prevailing at the date of their calculation;

• Ex-post returns are inversely correlated with change in risk aversion. All else being equal, an increase in anticipated risk leads to a decrease in the value of the assets, and hence in their actual ex-post yield. An increase in investor required return therefore results in a reduction in the ex-post risk premium while the ex-ante risk premium increases: the ex-post risk premium thus varies in contrast to the risk aversion of economic agents. Conversely, the ex-ante risk premium rises when the feeling of uncertainty increases, as it measures the "price of risk";
• Past returns incorporate good and bad news that have affected a stock price. Thus, effective market returns incorporate defaults that have resulted in recapitalizations or bankruptcy. In this sense, the ex-post premium is "net" of the default risk which lowers the market's effective return. Conversely, analysts' forecasts are generally established assuming a company's survival and therefore do not integrate any probability of default. These are therefore not mathematical expectations according to the CAPM. Forward-looking premiums correct structurally this bias as well as other optimism biases in the production of forecasts, unlike historical premiums. Historical premiums are thus inadequate for discounting generally biased forecasts.

The most extensive and achieved approach for calculating the ex-ante risk premium is to replicate for each security an evaluation model identical to that used for valuing a company by the DCF method. On the basis of a series of forecast cash flows and the share's market value, the IRR  satisfies the following formula:

 

where V is the company's equity market capitalization, ECF_t the annual equity cash flow and ECF_n normalized cash flow to infinity, with growth to perpetuity g.

 

 

where NR is the net result, D&A is depreciation and amortization, Inv the capital expenditures, Δ changes in working capital, net financial debt, provisions and unrealized gains (excluding disposals), and PV the result on asset disposals.

 

Based on analysts' forecasts, we establish a reasonable consensus for the first three years. We then extrapolate these forecasts over two years to converge growth towards the rate (g) used to calculate the terminal value.

 

This long-term growth rate is lower than the nominal growth expected for the economy as a whole. It is thus inferior to the sum of expected effective growth and inflation in accordance with current practice, with the aim of replicating as accurately as possible the evaluation model usually used by appraisers to provide them with a tool adapted to their needs.

 

In practice, given the quality of the information available about analyst forecasts, we do not directly calculate the market IRR using formula 2, but go through an intermediate calculation step using an APV approach, described in detail in methodological note # 5.